スマスロ北斗の拳には優遇と冷遇が有ると言われているが、デキレなのか?
もしあればATの継続率などは実践データとメーカ公表値で乖離が出ているのではないか?
これを後述する実践データと公表値から計算される理論値とを比較し検証してみた。
本検証では以下順序でメーカ公表値からのATの継続率の理論値と実践データでの継続率を比較し検証を実施している。
①:AT中に上乗せする確率を求める。
②:最終的な単発終了確率を算出する。
③:実践データからの単発終了割合と比較検証する。
①AT中に上乗せする確率
本機のATは前半パートが30Gでメダルが増加する区間、後半パートが継続バトルで8ゲームの減算区間になっています。
AT中は宿命バトル勝利による上乗せや、継続バトル中の書き換え抽選があり、実際は選択された継続率より少し上がります。
下記はAT前半パートでの宿命バトル発展率です。まずはそこから前半パートでの上乗せ確率を計算していきます。
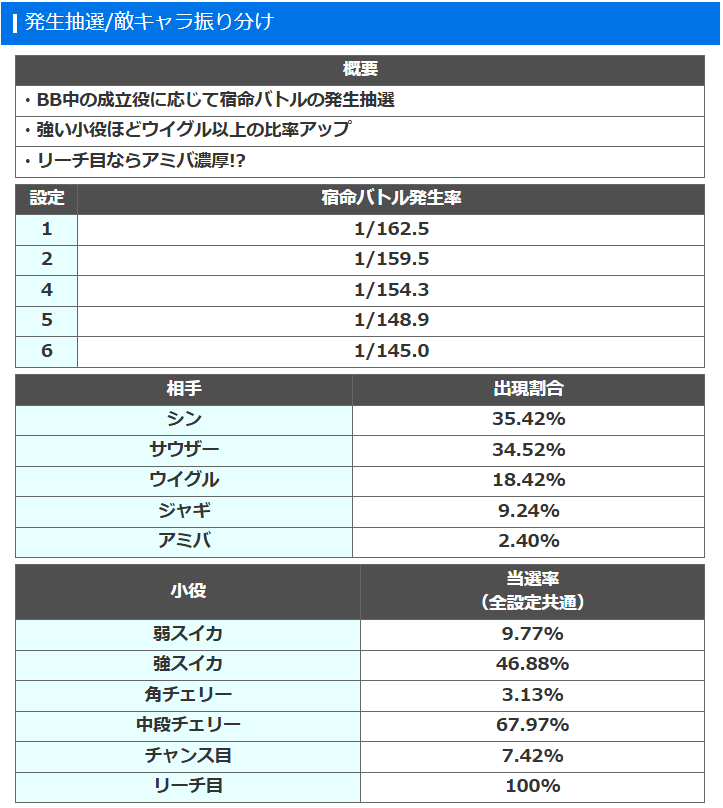
ホールでの設定は基本的にはほぼ設定1ですが、全体の設定状況を考慮して設定2の発展確率で計算していきます。
| パターン | 計算式 | 勝率 | 確率 (q) |
|---|---|---|---|
| シン | 16.44% × 35.42% × 19.92% | 19,92% | 1.16% |
| サウザー | 16.44% × 34.52% × 30.29% | 30.29% | 1.72% |
| ウイグル | 16.44% × 18.42% × 51.41% | 51.41% | 1.56% |
| ジャギ | 16.44% × 9.24% × 90.38% | 90.38% | 1.37% |
| アミバ | 16.44% × 2.40% × 100% | 100% | 0.39% |
1回の試行で1/159.5を引く確率 (p)
\[ p = 1 / 159.5 \approx 0.00627 (0.627%) \]
30回の試行で1回以上成功する確率
\[ P(成功) = 1 - (1 - p)^{30} \approx 1 - 0.8356 \approx 0.1644 (16.44%) \]
振り分け率の適用
上記の表での勝率とはwebで公開されている宿命バトルでの勝利確率です。
さらに、各対戦相手で計算をすると前半パートで宿命バトルに突入し勝利する確率は(q)は表のようになります。
各振り分けを合算すると、
\[ P(総合) = 1.16% + 1.72% + 1.56% + 1.37% + 0.39% = 6.20% \]
結論
したがって、初当たり時のAT中の前半パートで上乗せする確率は 6.20% です。
さらにATの継続バトル中の強チェリーによる継続もあります。
計算したところ、8Gで1/240(設定1:強チェリー🍒確率)を引く確率は3.3%あるそうです。結構ありますね?
他の確定役やスイカ等でも抽選は有りますが、影響は少ないはずなので今回は省略します。
★天井について
天井到達率については、以下のWeb上のデータを参考にすると下記になります。
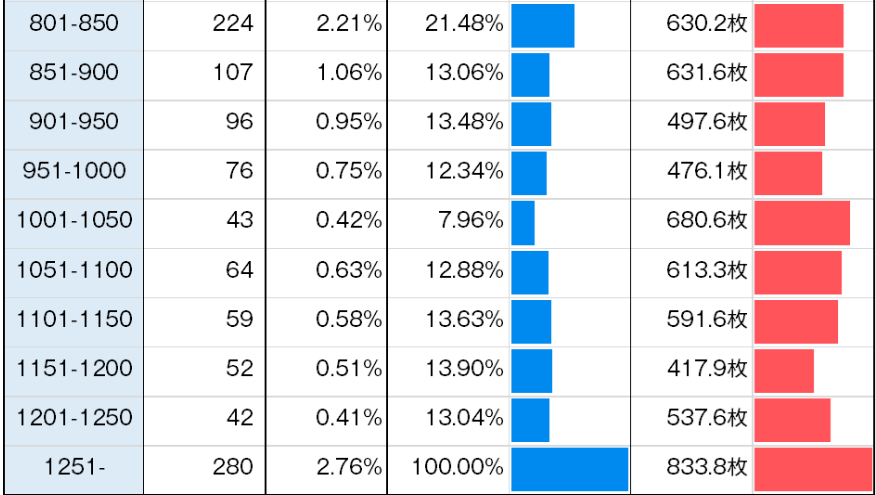
- リセット後に 800G以上ハマる確率:10.28%
- 1251Gハマる確率:2.76%
ここでは後述する北斗揃い確率に天井到達も含まれていると考え、天井到達分は除外して計算します。
② 最終的なAT単発終了確率
次に赤7揃い時の初回継続率について下記振り分けを基に計算していきます。
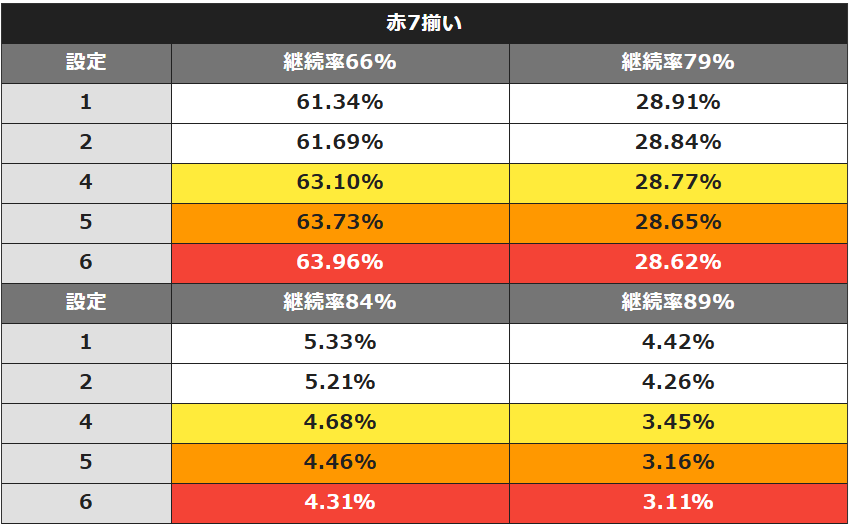
100から各継続率を引いた数値が上乗せを除いた赤7揃い時の初回非継続率になります。
- パターンA:66%継続:100 - 66 = 34%
- パターンB:79%継続:100 - 79 = 21%
- パターンC:84%継続:100 - 84 = 16%
- パターンD:89%継続:100 - 89 = 11%
次に各継続率で初戦で負けて非継続となる確率に、下記の上乗せ確率を加味して計算していきます。
- AT中の上乗せ確率:6.20%
- AT継続バトル中の上乗せ確率:3.30%
最終的にAT単発終了となる条件は
「赤7揃い時に初回非継続に当選し、且つ前半パートと後半のバトルで上乗せしないこと」
となりますのでこの条件になる確率を計算していきます。
計算手順
各継続率(パターンA~D)で「非継続する」と上乗せ抽選に「いずれも当選しない」を両方満たす確率を求め全部合算したものが
初回継続しない確率〈ATが単発終了する確率〉となります。
パターンA: 66% ⇒ 6.2% ⇒ 3.3%
- 1回目の外れる確率 = ( 1 - 0.66 = 0.34 )
- 2回目の外れる確率 = ( 1 - 0.062 = 0.938 )
- 3回目の外れる確率 = ( 1 - 0.033 = 0.967 )
全て外れる確率: P(全て外れる) = 0.34 × 0.938 × 0.967
計算:
- 0.34 × 0.938 = 0.31892
- 0.31892 × 0.967 = 0.3081
少なくとも1つに当選する確率: P(いずれか当選) = 1 - 0.3081 = 0.6919
結果: 約69.19%
パターンB: 79% ⇒ 6.2% ⇒ 3.3%
- 1回目の外れる確率 = ( 1 - 0.79 = 0.21 )
- 2回目の外れる確率 = ( 1 - 0.062 = 0.938 )
- 3回目の外れる確率 = ( 1 - 0.033 = 0.967 )
全て外れる確率: P(全て外れる) = 0.21 × 0.938 × 0.967
計算:
- 0.21 × 0.938 = 0.19698
- 0.19698 × 0.967 = 0.1904
少なくとも1つに当選する確率: P(いずれか当選) = 1 - 0.1904 = 0.8096
結果: 約80.96%
パターンC: 84% ⇒ 6.2% ⇒ 3.3%
- 1回目の外れる確率 = ( 1 - 0.84 = 0.16 )
- 2回目の外れる確率 = ( 1 - 0.062 = 0.938 )
- 3回目の外れる確率 = ( 1 - 0.033 = 0.967 )
全て外れる確率: P(全て外れる) = 0.16 × 0.938 × 0.967
計算:
- 0.16 × 0.938 = 0.15008
- 0.15008 × 0.967 = 0.1452
少なくとも1つに当選する確率: P(いずれか当選) = 1 - 0.1452 = 0.8548
結果: 約85.48%
パターンD: 89% ⇒ 6.2% ⇒ 3.3%
- 1回目の外れる確率 = ( 1 - 0.89 = 0.11 )
- 2回目の外れる確率 = ( 1 - 0.062 = 0.938 )
- 3回目の外れる確率 = ( 1 - 0.033 = 0.967 )
全て外れる確率: P(全て外れる) = 0.11 × 0.938 × 0.967
計算:
- 0.11 × 0.938 = 0.10318
- 0.10318 × 0.967 = 0.0998
少なくとも1つに当選する確率: P(いずれか当選) = 1 - 0.0998 = 0.9002
結果: 約90.02%
よって**実質的な継続率**は以下になりました。
- - 66%継続の実質継続率 (66% ⇒ 6.2% ⇒ 3.3%): 約69.19%
- - 79%継続の実質継続率 (79% ⇒ 6.2% ⇒ 3.3%): 約80.96%
- - 84%継続の実質継続率 (84% ⇒ 6.2% ⇒ 3.3%): 約85.48%
- - 89%継続の実質継続率 (89% ⇒ 6.2% ⇒ 3.3%): 約90.02%
そこから各継続率(パターンA~D)の選択率の振り分けを見ると、設定1では以下の割合となります。
- パターンA選択率:66%:61.34%
- パターンB選択率:79%:28.91%
- パターンC選択率:84%:5.33%
- パターンD選択率:89%:4.42%
当選しない確率の計算
以下は、4つの異なる継続確率と選択率を基に、1度だけ抽選を実施した場合の継続しない確率の計算結果です。
計算手順
- 各選択肢の外れる確率を計算します。
- 外れる確率と選択率を掛け合わせて、各選択肢の全体に占める「外れる確率」を求めます。
- 全体の継続しない確率は、各選択肢の「外れる確率」の合計です。
計算詳細
選択A
- 継続確率: 69.19%
- 外れる確率: \( 1 - 0.6919 = 0.3081 \)
- 選択率: 61.34%
- 全体に占める外れる確率: \( 0.6134 × 0.3081 = 0.1891 \)
選択B
- 継続確率: 80.96%
- 外れる確率: \( 1 - 0.8096 = 0.1904 \)
- 選択率: 28.91%
- 全体に占める外れる確率: \( 0.2891 × 0.1904 = 0.0550 \)
選択C
- 継続確率: 85.48%
- 外れる確率: \( 1 - 0.8548 = 0.1452 \)
- 選択率: 5.33%
- 全体に占める外れる確率: \( 0.0533 × 0.1452 = 0.0077 \)
選択D
- 継続確率: 90.02%
- 外れる確率: \( 1 - 0.9002 = 0.0998 \)
- 選択率: 4.42%
- 全体に占める外れる確率: \( 0.0442 × 0.0998 = 0.0044 \)
全体の当選しない確率
全体の外れる確率を合計します:
- \( 0.1891 + 0.0550 + 0.0077 + 0.0044 = 0.2562 \)
結果: AT単発終了確率は約25.62% となりました!
しかし、ここで北斗揃いの影響を考慮する必要があります。
面倒くさいので北斗揃いは2連以上確定とします。※単発率も北斗揃い率も両方低いため
北斗揃い率は 1/7274 となっています。
- 設定1:初当たり率 1/383.4、北斗揃い率 1/7274.0
- 設定2:初当たり率 1/370.5、北斗揃い率 1/7274.0
これを基にAT当選時に赤7揃いとなる確率を計算すると、下記のようになります。
- 設定1:94.73%
- 設定2:94.91%
この確率を単発終了確率に適用すると、
- 設定1:25.62 × (94.73 / 100) = 24.27%
最終的な確率は、24.3% とします。これがAT1回あたりに単発終了する確率となります。
※設定2も大差ないため上記の数字とします。
③ 獲得枚数分布からの単発割合の考察
では実際のデータから単発終了の割合が全ATの24.3%になっているかを検証していきます。
下記は実践データから得られた獲得枚数の分布などの結果です。
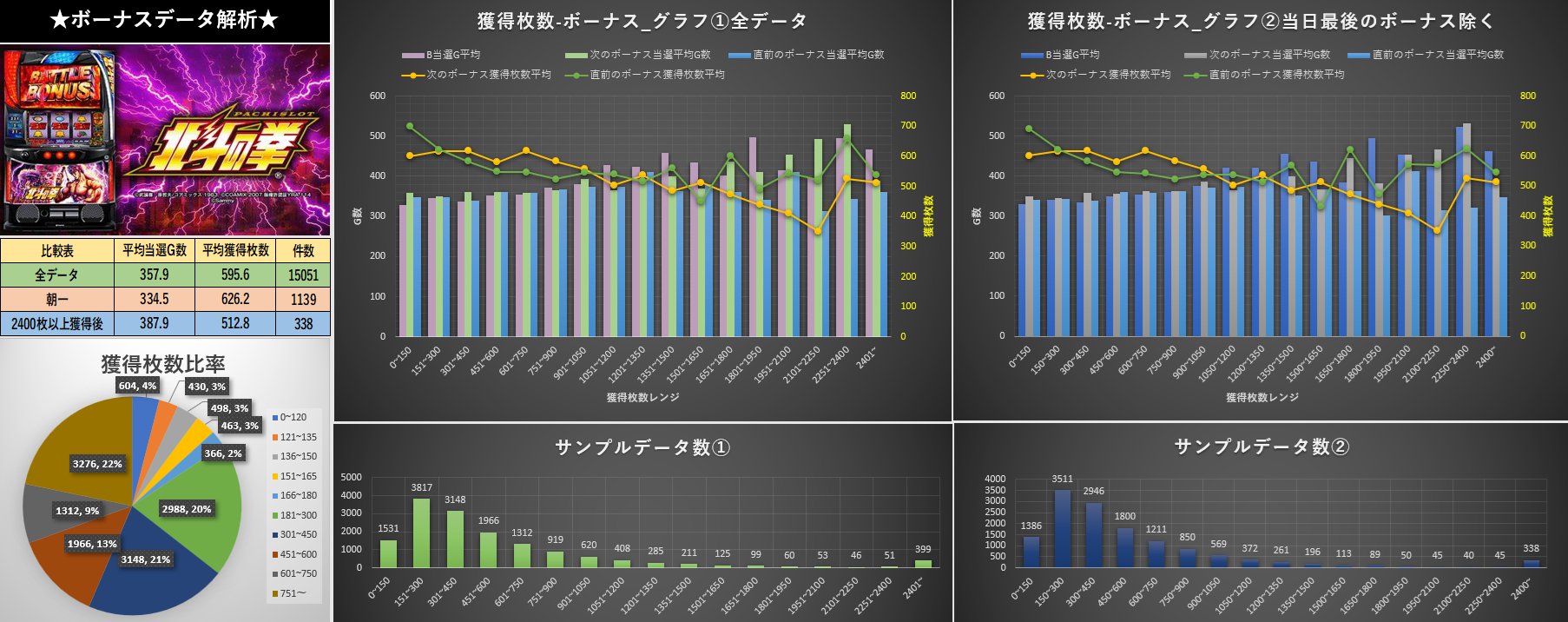
単発とみなされるケースの獲得枚数分布は以下の通りです。
※AT継続毎の獲得枚数ではなく開始から終了までの獲得枚数を合算して取得していたのでこの方法になってしまいます。。
| 獲得枚数 | 件数 | 割合 |
|---|---|---|
| 0~120枚 | 604 | 4.01% |
| 121~135枚 | 430 | 2.86% |
| 136~150枚 | 498 | 3.31% |
| 151~165枚 | 463 | 3.08% |
| 166~180枚 | 366 | 2.43% |
ATの純増枚数は 4.1枚 で、減算区間(データ上は10G、単発が目的なので無視しても良いかも)を考慮すると、
4.1枚*30GA+4.1*1/6(宿命バトル突入率16.6%位でしたね)*2(宿命バトルのG数)-10Gでの減算枚数(通常時は50枚あたり50Gとします)
124.3+1.36-10=115.66 ※宿命バトル2度突入などは含めません。
AT1回あたりの平均獲得枚数は 115.7枚 となります。
120枚以下を単発とすると実践データから割合はたったの4%しかありません。さすがにこれはおかしいので
獲得枚数分布から165枚以下で終了している場合を単発とします。その場合、割合は 13.25% です。
実際は2連しても165枚以下しか獲得できないケースや、逆に単発で200枚近く取れるケースもあるので相殺して165枚としています。
仮に180枚以下とした場合の単発終了割合は 15.69% となります。また実践データには北斗揃いも含まれています。
上記を考慮しても実際の単発割合は 14%~15% 位となる可能性が高いです。
★ 最終結果 ★
- 計算上のAT単発終了確率:24.3%
- 実践値からの単発確率:14%~15%
計算と実践値の差異を考慮すると、継続率以外の要因が影響している可能性が高いです。
つまり、 優遇や冷遇が存在し、獲得枚数が管理されている可能性が高い という結論に至りました。
◆ 獲得枚数分布からの「優遇・冷遇」考察 ◆
上記の結果でも十分かもしれませんが、念のためグラフからも検証してみます。
■ グラフの見方
X軸の数値はボーナス、つまりATでの獲得枚数です。棒グラフでATの獲得枚数毎のゲーム数Y軸左側の数値で表しています。
線グラフではX軸の各AT(獲得枚数毎)のその前後のATでの獲得枚数Y軸右側の数値で表しています。
リセット後は1つ前のATが存在しないため、除外しています。
右のグラフでは各データ取得日での最後のATを除いた数値を表しています。
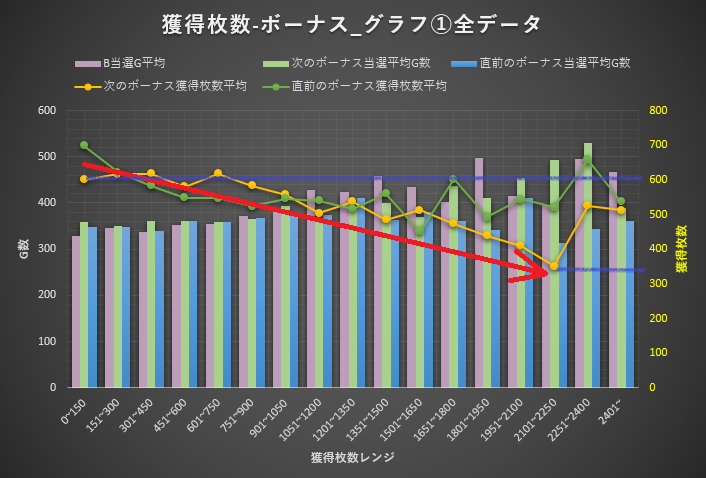
◆ グラフからの考察
「獲得枚数-ボーナス_グラフ」は2種類ありますがどちらも獲得枚数が増えるにつれて次のATでの獲得枚数が下がっている(黄色い線グラフ)ことが分かります。
→ 獲得枚数が多いと次のATが冷遇されているとなりますね。
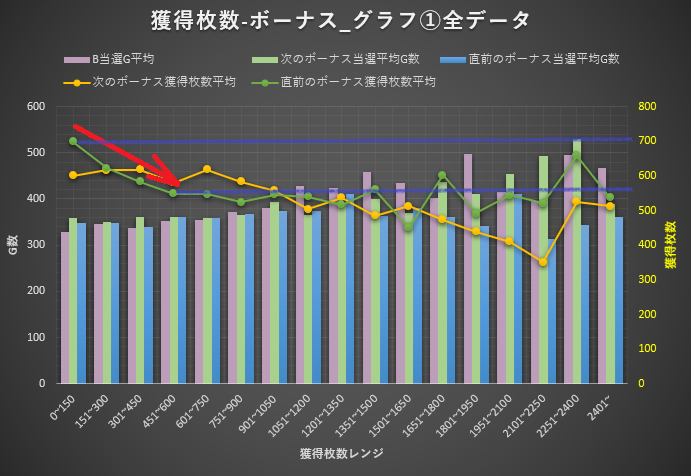
終了したATの直前の平均獲得枚数が700枚位であるの対し、
450枚~600枚獲得して終了したATの直前の獲得枚数平均が約550枚
となっていますので150枚ほど平均に差があることになります。
これ以上の獲得枚数には差はあまりありませんが、
「前回獲得枚数が多いと次のATの獲得が少なくなっている」と示すには
十分な結果ではないでしょうか。
ここからも→ 冷遇、もしくは調整していることが読み取れると思います。
もし、どのGで当選しても等しく継続抽選がされている場合、黄色い線や緑の線はともに水平に近い線を描くはずです。
ちなみに2000枚超えの次回獲得枚数が高いのは、貫きによる北斗揃いスタートが影響しているためです。
・結論
上記のグラフからも優遇と冷遇の存在がわかると思います。つまり★デキレ★は有りますとなりますね。
